
Q 3: the state to which M goes when the third 1 is read from the string Q 2: the state to which M goes when the second 1 is read from the string Q 1: the state to which M goes when the first 1 is read from the string
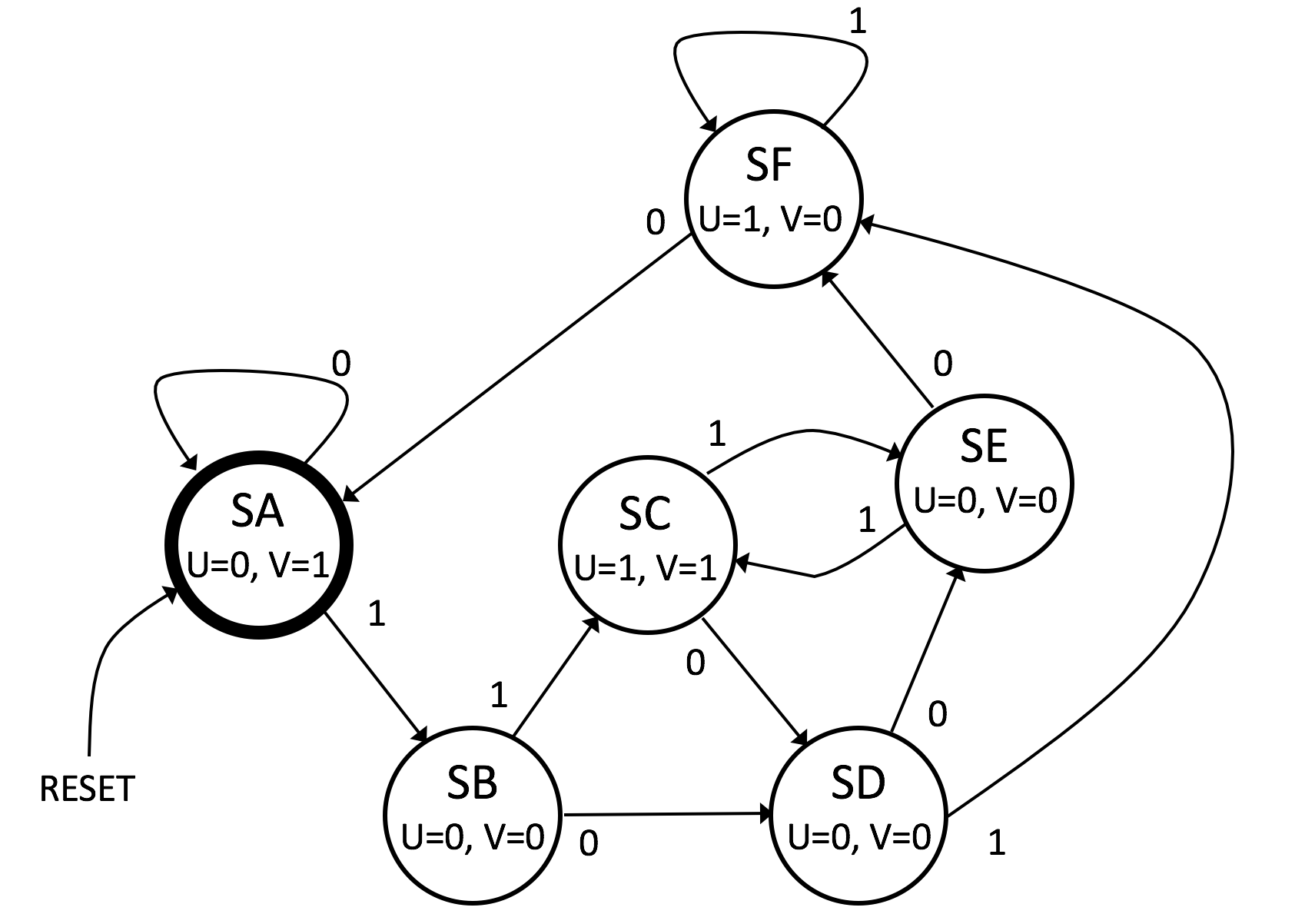
The automaton M must have at least four distinct states: Now consider the problem of starting with a description of a languageand designing an automaton to accept exactly that language.ĭesign a finite-state automaton that accepts the set of all strings of 0's and 1's containing exactly three 1's. A machine may accept several strings, but it always accepts only one language.
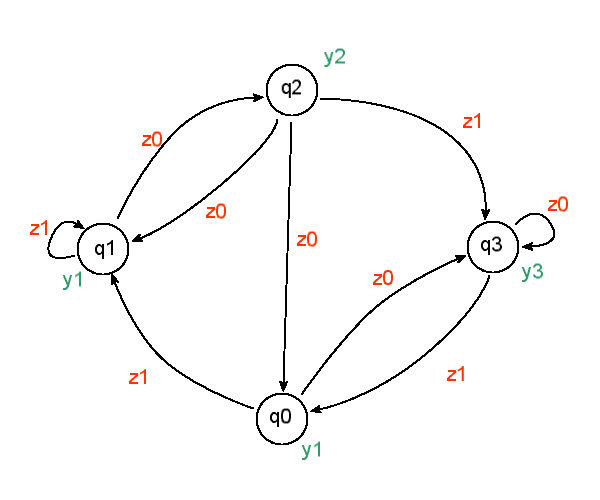
When a machine accepts a language, that language is the collection of all strings which the machine will accept. If A is the set of strings that a machine N accepts, we say that A is the language of machine N and write L( N) = A. This means that M rejects that particular input. In this case, the final state of M would be q 2, which is not an accept state. The transitions would be the same up to step 6, where the transition function would be replaced with T( q 1, 0) q 2. Suppose that instead of the above example, we had fed in the string 10010. On any input string w, if the transition doesn't reach an accept state at the end of the input, it means that the machine rejects the input. accept because M is in accept state q 1at the end of the input. read 1, follow transition from q 1to q 1 ħ. read 1, follow transition from q 2to q 1 Ħ. read 0, follow transition from q 1to q 2 ĥ. read 0, follow transition from q 0to q 1 Ĥ. read 1, follow transition from q 0to q 0 ģ. When the input string 10011 is fed to machine M, the processing proceeds as follows:Ģ. Practice ExercisesĬonsider the automaton (machine) M shown below. You can check this by comparing the transition table with the above state diagram. For instance if q 0 is the current state and 0 is the current input symbol, then the transition function is T( q 0, 0) q 1. The transition function can be represented as T(current state, current input symbol) next state. The transition function T can be described by a transitionfunction table, as follows: State/Input Symbol In this case, Q = and q 0is the start state. For instance, a finite automaton M is shown in the state diagram below. The operation of a finite-state automaton is always illustrated in a state diagram.
For each pair of "current state" and "current input symbol" (the function input), the transition function produces as output the next state in the automaton. The transition function defines the movement of an automaton from one state to another by treating the current state and current input symbol as an ordered pair. Q 0 : the start state of the automaton, q 0 Q. : a finite set of input symbols, called alphabet. Q : a finite set of states the automaton can be in. Application of Functions: Finite-State Automataĭefinition of A Finite-State Automaton | Languages Accepted by An AutomatonĪ finite-state automaton is comprised of a set of five objects ( Q,, q 0, F, T) where: 1.


 0 kommentar(er)
0 kommentar(er)
